The rendering equation for PhySG, along a view-direction $o$ from camera, is defined as follows: \(R(o) = \int_{S^2} L(i) \rho_o(i) max(0, i.n) di\)

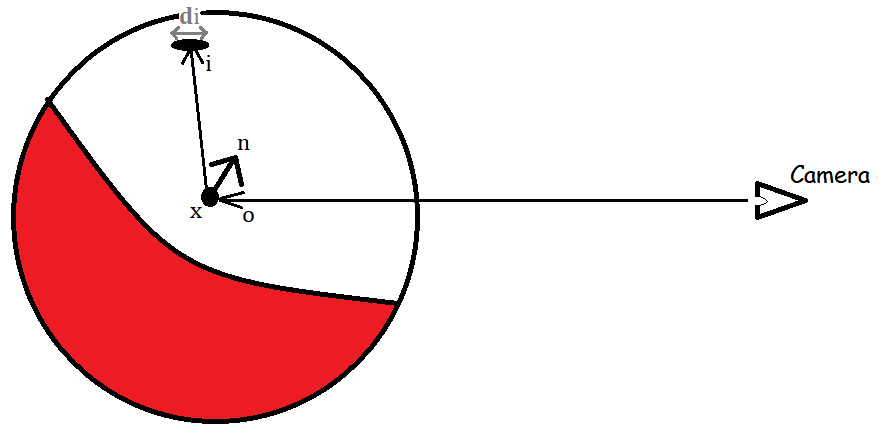
Using Spherical Gaussians (SGs) to render the scene is discussed in the previous post.

The mathematical properties of SGs are discussed before.

PhySG in equations

\(\rho_d(i) = \frac{a(x)}{\pi}, \rho_s(i) = M_o(i)D(h)\), where $h = \frac{i + o}{||i + o||_2}$ \(\\M_o(i) = \frac{F(o,i)S(o,i)}{\pi(n.i)(n.o)}\) \(\\F(o,i) = s + (1-s).2^{-(5.55473o.h+6.8316)(o.h)}\) \(\\S(o,i) = \frac{o.n}{o.n(1-k)+k}.\frac{i.n}{i.n(1-k)+k}\) where $k = \frac{(R+1)^2}{8}$, $R$ is the roughness, $s$ is the specular reflectance \(\\D(h) = \frac{1}{\pi R^4}e^{-(cos^{-1}(h.n)/R)^2} \approx G(h; n, \frac{2}{R^4}, \frac{1}{\pi R^4})\)

To calculate $M_o(i)$: \(\\\)We can approximate $i \approx 2(o.n)n - o$. \(\\\)So $h=n$, or $F(o,i) = s + (1-s)2^{-(5.55473o.n+6.8316)(o.n)}$. \(\\\)Also, $S(o,i) = \frac{o.n}{o.n(1-k)+k}.\frac{(2(o.n)n - o).n}{(2(o.n)n - o).n(1-k)+k}$. \(\\M_o(i) = \frac{s + (1-s)2^{-(5.55473o.n+6.8316)(o.n)} . \frac{o.n}{o.n(1-k)+k}.\frac{2(o.n)n.n - o.n}{(2(o.n)n.n - o.n)(1-k)+k}}{\pi(2(o.n)n.n - o.n)(n.o)}\)

To calculate $D(h)$: \(\\\)Note, $D()$ is a function of the half vector $h$. So, it must be spherically warped to be a function of the incident light direction $i$. \(\\D^*(i) = G(i; p_D, \lambda_D, \mu_D)\) where $p_D$ is the lobe orientation of the SG, $\lambda_D$ is the lobe sharpness of the SG, and $\mu_D$ is the lobe amplitude of the SG.

The spherical warp transformation is defines as: \(\\i = \psi(h) = 2(o.h)h - o\) where $\psi()$ is the spherical warp transformation.

This follows: \(\\p_D = \psi(n) = 2(o.n)n - o\) \(\\\lambda_D = \frac{\frac{2}{R^4}}{\tau(h)} = \frac{2}{4|o.h|R^4}\) \(\\\mu_D = \frac{1}{\pi R^4}\)

Therefore \(\rho_s(i) = M_o(i)D^*(i) \approx G(i; p_D, \lambda_D, M_o(i)*\mu_D)\)

Feeding all into Equation 1, we get: \(R(o) = \int_{S^2} \sum_{j=1}^N G(i; p_j, \lambda_j, \mu_j)(\frac{a(x)}{\pi} + G(i; p_D, \lambda_D, M_o(i)*\mu_D))(G(i; n, 0.0315, 32.7080) - 31.7003) di\)

\(\\= \frac{a(x)}{\pi}\int_{S^2} \sum_{j=1}^N G(i; p^1_j, \lambda^1_j, \mu^1_j)di - \frac{a(x)}{\pi}\int_{S^2} \sum_{j=1}^N G(i; p^2_j, \lambda^2_j, \mu^2_j)di\) \(\\+\int_{S^2} \sum_{j=1}^N G(i; p^3_j, \lambda^3_j, \mu^3_j)di - \int_{S^2} \sum_{j=1}^N G(i; p^4_j, \lambda^4_j, \mu^4_j)di\)

To summarize: \(R(o) = Term_1 - Term_2 + Term_3 - Term_4\)

\(\\Term_1 = \frac{a(x)}{\pi}\int_{S^2} \sum_{j=1}^N G(i; p^1_j, \lambda^1_j, \mu^1_j)di\) \(\\p^1_j = \frac{\lambda_j n + 0.0315 p_j}{\lambda_j + 0.0315}\) \(\\\lambda^1_j = \lambda_j + 0.0315\) \(\\\mu^1_j = \mu_j * 32.7080\) \(\\Term_1 = 32.7080 * \frac{a(x)}{\pi} * \mu_j \int_{S^2} \sum_{j=1}^N e^{(\lambda_j + 0.0315)(i.\frac{\lambda_j n + 0.0315 p_j}{\lambda_j + 0.0315} - 1)}di\)

\(\\Term_2 = \frac{a(x)}{\pi}\int_{S^2} \sum_{j=1}^N G(i; p^2_j, \lambda^2_j, \mu^2_j)di\) \(\\p^2_j = p_j\) \(\\\lambda^2_j = \lambda_j\) \(\\\mu^2_j = \mu_j * 31.7003\) \(\\Term_2 = 31.7003 * \frac{a(x)}{\pi} * \mu_j \int_{S^2} \sum_{j=1}^N e^{\lambda_j(i.p_j - 1)}di\)

\(\\Term_3 = \int_{S^2} \sum_{j=1}^N G(i; p^3_j, \lambda^3_j, \mu^3_j)di\) \(\\p^3_j = \frac{\lambda^1_j p_D + \lambda_D p^1_j}{\lambda^1_j + \lambda_D}\) \(= \frac{(\lambda_j + 0.0315) (2*(o.n)n-o) + \frac{2}{4|o.h|R^4}\frac{\lambda_j n + 0.0315 p_j}{\lambda_j + 0.0315}}{\lambda_j + 0.0315 + \frac{2}{4|o.h|R^4}}\) \(\\\lambda^3_j = \lambda_j + 0.0315 + \lambda_D = \lambda_j + 0.0315 + \frac{2}{4|o.h|R^4}\) \(\\\mu^3_j = \mu_j * 32.7080 * M_o(i) * \mu_D = \mu_j * 32.7080 * \frac{s + (1-s)2^{-(5.55473o.n+6.8316)(o.n)} . \frac{o.n}{o.n(1-k)+k}.\frac{2(o.n)n.n - o.n}{(2(o.n)n.n - o.n)(1-k)+k}}{\pi(2(o.n)n.n - o.n)(n.o)} * \frac{1}{\pi R^4}\) \(\\Term_3 = \mu_j * 32.7080 * \frac{s + (1-s)2^{-(5.55473o.n+6.8316)(o.n)} . \frac{o.n}{o.n(1-k)+k}.\frac{2(o.n)n.n - o.n}{(2(o.n)n.n - o.n)(1-k)+k}}{\pi(2(o.n)n.n - o.n)(n.o)} * \frac{1}{\pi R^4} \int_{S^2} \sum_{j=1}^N e^{(\lambda_j + 0.0315 + \frac{2}{4|o.h|R^4})(i.\frac{(\lambda_j + 0.0315) (2*(o.n)n-o) + \frac{2}{4|o.h|R^4}\frac{\lambda_j n + 0.0315 p_j}{\lambda_j + 0.0315}}{\lambda_j + 0.0315 + \frac{2}{4|o.h|R^4}} - 1)}di\)

\(\\Term_4 = \int_{S^2} \sum_{j=1}^N G(i; p^4_j, \lambda^4_j, \mu^4_j)di\) \(\\p^4_j = \frac{\lambda^2_j p_D + \lambda_D p^2_j}{\lambda^2_j + \lambda_D}\) \(= \frac{\lambda_j (2*(o.n)n-o) + \frac{2}{4|o.h|R^4}p_j}{\lambda_j + \frac{2}{4|o.h|R^4}}\) \(\\\lambda^4_j = \lambda_j + \frac{2}{4|o.h|R^4}\) \(\\\mu^4_j = \mu_j * 31.7003 * M_o(i) * \mu_D = \mu_j * 31.7003 * \frac{s + (1-s)2^{-(5.55473o.n+6.8316)(o.n)} . \frac{o.n}{o.n(1-k)+k}.\frac{2(o.n)n.n - o.n}{(2(o.n)n.n - o.n)(1-k)+k}}{\pi(2(o.n)n.n - o.n)(n.o)} * \frac{1}{\pi R^4}\) \(\\Term_4 = \mu_j * 31.7003 * \frac{s + (1-s)2^{-(5.55473o.n+6.8316)(o.n)} . \frac{o.n}{o.n(1-k)+k}.\frac{2(o.n)n.n - o.n}{(2(o.n)n.n - o.n)(1-k)+k}}{\pi(2(o.n)n.n - o.n)(n.o)} * \frac{1}{\pi R^4} \int_{S^2} \sum_{j=1}^N e^{(\lambda_j + \frac{2}{4|o.h|R^4})(i.\frac{\lambda_j (2*(o.n)n-o) + \frac{2}{4|o.h|R^4}p_j}{\lambda_j + \frac{2}{4|o.h|R^4}} - 1)}di\)