A spherical Gaussian is a function defined on the surface of a sphere. It is defined as follows:

where $v \in S^2$ is the input vector, $\mu \in R$ is the lobe amplitude, $\lambda \in R$ is the lobe sharpness, and $p \in S^2$ is the lobe orientation.

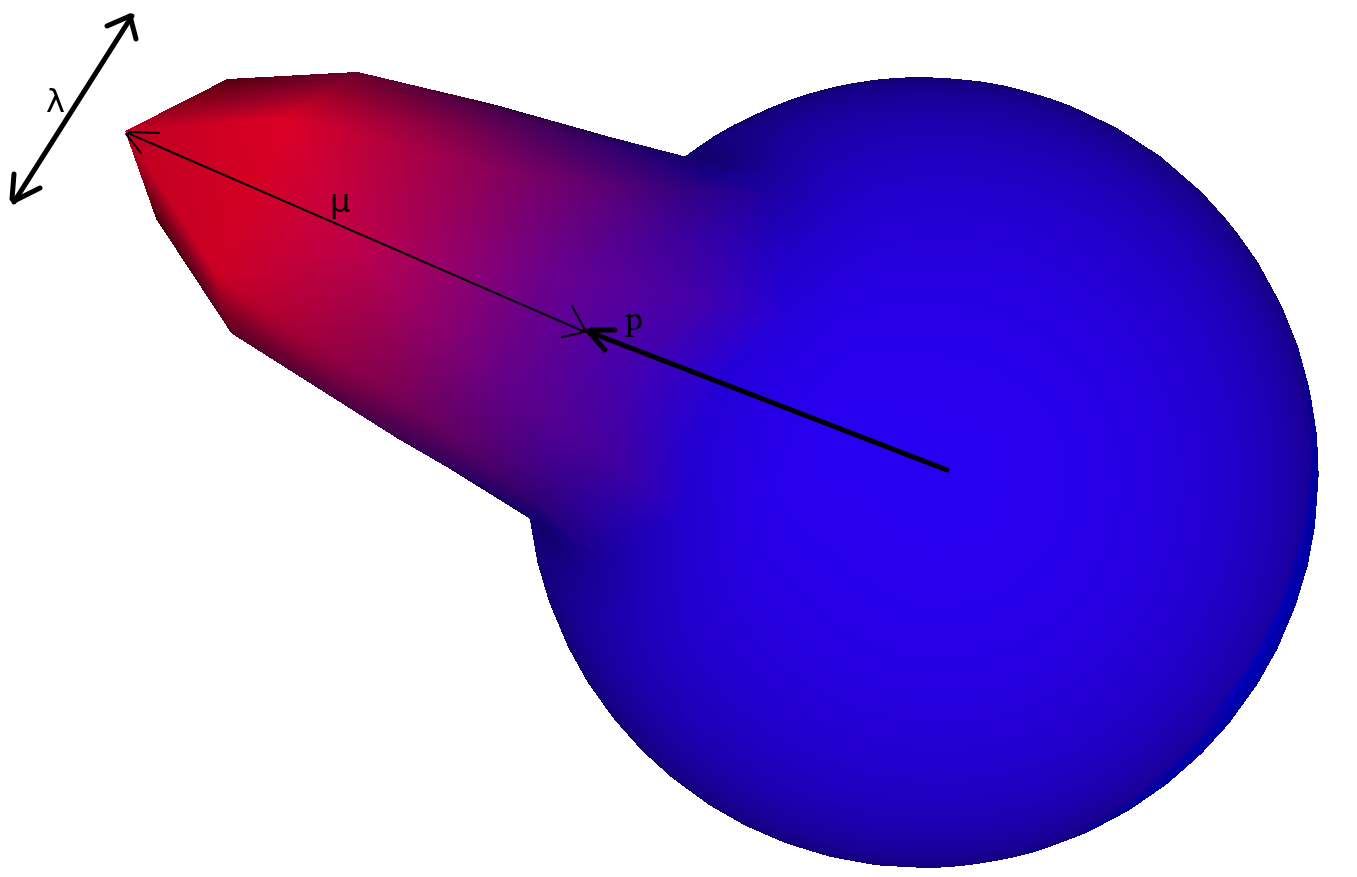
The spherical Gaussian is a generalization of the Gaussian function, which is defined on the plane. The spherical Gaussian is a function of the dot product of the input vector and the lobe orientation. The lobe orientation is a vector that defines the direction of the lobe. The lobe sharpness is a parameter that controls the width of the lobe. The lobe amplitude is a parameter that controls the height of the lobe.

The total energy of the spherical Gaussian is 1. i.e., \(\int_{S^2} G(v; p, \lambda, \mu) dv = 1\)

Some mathematical properties of spherical Gaussians

Product of 2 spherical Gaussians is a spherical Gaussian:

\(G(v; p, \lambda, \mu) G(v; p', \lambda', \mu') = G(v; p_m, \lambda_m, \mu_m)\)

Proof: \(G(v; p, \lambda, \mu) G(v; p', \lambda', \mu') \\= \mu \mu' e^{\lambda(p.v-1)} e^{\lambda'(p'.v-1)} \\= \mu \mu' e^{(\lambda p.v + \lambda'p'.v) - (\lambda + \lambda')} \\= \mu\mu'e^{(\lambda + \lambda')(\frac{\lambda p + \lambda'p'}{\lambda + \lambda'}.v - 1)}\)

where $p_m = \frac{\lambda p + \lambda’p’}{\lambda + \lambda’}$, $\lambda_m = \lambda + \lambda’$ and $\mu_m = \mu\mu’$

Mixture model of scattered spherical Gaussians:

\(F^*(v) = \sum_{i=1}^N w_i G(v; p_i, \lambda_i, \mu_i)\)

where $w_i$ is the weight of the $i^{th}$ spherical Gaussian, $p_i$ is the lobe orientation of the $i^{th}$ spherical Gaussian, $\lambda_i$ is the lobe sharpness of the $i^{th}$ spherical Gaussian, and $\mu_i$ is the lobe amplitude of the $i^{th}$ spherical Gaussian.

An SG mixture model is closed under rotations. \(R \circ F^*(v) = \sum_{i=1}^N w_i G(v; R \circ p_i, \lambda_i, \mu_i)\)

where $R$ is a rotation matrix.

Similarly, multiplication of all SGs of a mixture model with a constant. \(\sum_{i=1}^N c*w_i G(v; p_i, \lambda_i, \mu_i) = c*F^*(v) = \sum_{i=1}^N w_i G(v; p_i, \lambda_i, c * \mu_i)\)

where $c$ is a constant.