The rendering equation, along a view-direction $o$ from camera, is defined as follows:

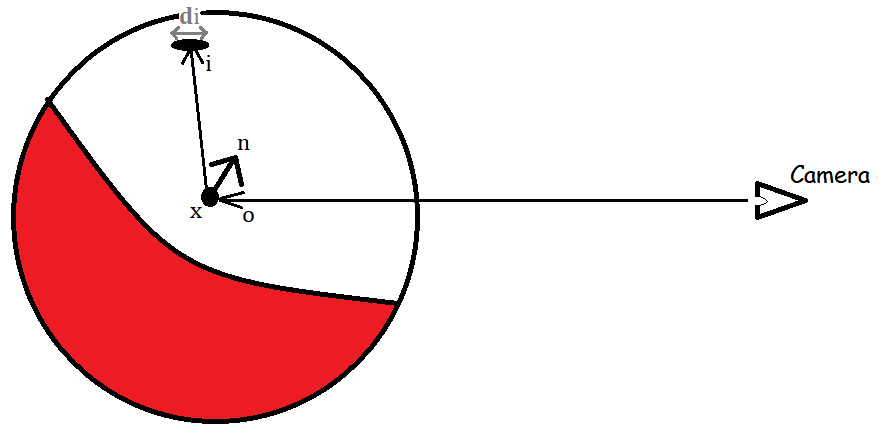
This rendering equation gives the final rendered color for a surface point $x$, illuminated by one or more light sources.

Here, $i$ is the incident light direction.

So, $L(i)$ defines direct illumination from light, $V(i)$ determines if the visibility of the light source, $\rho_o(i)$ is the Bidirection Radial Distribution Function (BRDF) that determines the albedo, diffuse and specularity, and $i.n$ gives the cosine angle between the surface and incident light direction.

Note, in this equation, we use $max(0, i.n)$ to only sample incident lights from positive hemisphere towards the surface normal.

The rendering process can be optimized by using Spherical Gaussians (SGs) instead of the standard process of sampling the incident light directions. This is because SGs are a closed form function of the dot product of the incident light direction and the lobe orientation. This means that we can directly compute the integral in the rendering equation using the SGs. However, sampling the incident light directions is time-consuming, and we can avoid this by using SGs.

The mathematical properties of SGs are discussed in the previous post.

Rendering using SGs

We can define environment map $L(i)$ as a mixture model of SGs. The environment map is a function of the incident light direction $i$.
\(L(i) = \sum_{j=1}^N G(i; p_j, \lambda_j, \mu_j)\)

where $p_j$ is the lobe orientation of the $j^{th}$ SG, $\lambda_j$ is the lobe sharpness of the $j^{th}$ SG, and $\mu_j$ is the lobe amplitude of the $j^{th}$ SG.

Similarly, by defining the BRDF $\rho_o(i)$ and the cosine angle $i.n$ as a mixture model of SGs, we can compute the integral in the rendering equation using the SGs.

\(\rho_o(i) = \frac{a}{\pi} + \rho_s(i)\) where a is the albeto of the surface, and $\rho_s(i)$ is the specular component of the BRDF.

Thus, the diffuse component of the BRDF is defined as follows: \(R_d(o) = \sum_{j=1}^N\frac{a}{\pi} \int_{S^2} G(i; p_j, \lambda_j, \mu_j) V(i) max(0, i.n) di\)

Similarly, the specular component of the BRDF is defined as follows: \(R_s(o) = \sum_{j=1}^N\int_{S^2} G(i; p_j, \lambda_j, \mu_j) V(i) \rho_s(i) max(0, i.n) di\)

We can further define $\rho_s(i)$ as SGs, and compute the integral using the SGs.

According to the microfacet theory, the specular component of the BRDF is defined as follows: \(\rho_s(i) = M_o(i)D(h)\)

where $M_o(i)$ is the combination of microfacet shadowing and Fresnel reflection, and $D(h)$ is the microfacet distribution function.

Here, $h$ is the half vector between the incident light direction $i$ and the view direction $o$. \(h = \frac{i+o}{||i+o||}\) \(\\M_o(i) = \frac{F(o,i)S(o,i)}{\pi(n.i)(n.o)}\)

where $F(o,i)$ is the Fresnel reflection, $S(o,i)$ is the microfacet shadowing, and $n.i$ and $n.o$ are the cosine angle between the surface normal and the incident light direction and the view direction respectively.

We can define $D(h)$ as follows according the microfacet theory: \(D(h) = e^{-(arccos(h.n)/m)^2}\)

where $m$ is the roughness of the surface.

We can approximate this NDF with a single SG lobe as follows: \(D(h) = G(h; n, 2/m^2, 1)\)

Note, $D()$ is a function of the half vector $h$. So, it must be spherically warped to be a function of the incident light direction $i$. \(D^*(i) = G(i; p_D, \lambda_D, \mu_D)\)

where $p_D$ is the lobe orientation of the SG, $\lambda_D$ is the lobe sharpness of the SG, and $\mu_D$ is the lobe amplitude of the SG.

The spherical warp transformation is defines as: \(i = \psi(h) = 2(o.h)h - o\)

where $\psi()$ is the spherical warp transformation.

This follows: \(p_D = \psi(n) = 2(o.n)n - o\) \(\lambda_D = \frac{2/m^2}{\tau(n)}\) \(\mu_D = 1\)

Differential area of this warp, $\tau(h)$, is the determinant of the Jacobian matrix of the spherical warp transformation. \(\tau(h) = \frac{\partial i}{\partial h} = \frac{||\frac{\partial \psi(h)}{\partial \theta} X \frac{\partial \psi(h)}{\partial \phi}||}{||\frac{\partial h}{\partial \theta} X \frac{\partial h}{\partial \phi}||} = 4|h.o|\)

where $h(\theta, \phi)$ is the spherical coordinates of the half vector $h$, i.e., $(\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta)$.

Hence, \(\rho_s(i) = M_o(i)D(h) = M_o(i)D^*(i)\)

where $D^*(i)$ is the SG approximation of the microfacet distribution function.

Further simplification gives, \(\rho_s(i) = M_o(i)G(i; p_D, \lambda_D, \mu_D) = G(i; p_D, \lambda_D, M_o(i)*\mu_D)\)

where $p_D$ is the lobe orientation of the SG, $\lambda_D$ is the lobe sharpness of the SG, and $\mu_D$ is the lobe amplitude of the SG.

Thus, the specular component of the BRDF is defined as follows: \(R_s(o) = \sum_{j=1}^N\int_{S^2} \sum_{j=1}^N V(i) G(i; p_D, \lambda_D, M_o(i)*\mu_D) max(0, i.n) di\)

where $p_D$ is the lobe orientation of the SG, $\lambda_D$ is the lobe sharpness of the SG, and $\mu_D$ is the lobe amplitude of the SG.

Similarly, by emperical fitting methods, we can define $i.n$ as an SG: \(i.n = G(i; n, 0.0315, 32.7080) - 31.7003\)

where $n$ is the surface normal.

Thus, the diffuse component of the BRDF is defined as follows: \(R_d(o) = \frac{a}{\pi}\sum_{j=1}^N \int_{S^{2+}} G(i; p_j, \lambda_j, \mu_j) V(i) G(i; n, 0.0315, 32.7080) di \\ - \frac{a}{\pi}*31.7003\sum_{j=1}^N\int_{S^{2+}} G(i; p_j, \lambda_j, \mu_j) V(i)di\)

And the specular component of the BRDF is defined as follows: \(R_s(o) = \sum_{j=1}^N\int_{S^{2+}} G(i; p_j, \lambda_j, \mu_j) V(i) G(i; p_D, \lambda_D, M_o(i)*\mu_D) G(i; n, 0.0315, 32.7080) di \\ - 31.7003\sum_{j=1}^N\int_{S^{2+}} G(i; p_j, \lambda_j, \mu_j) V(i) G(i; p_D, \lambda_D, M_o(i)*\mu_D) di\)

where, $S^{2+}$ is the upper hemisphere of the surface normal direction $i$.

We already discussed how to calculate $M_o(i)$ before.

Parameters to learn are as follows:

• $a$ is the albedo of the surface.
• $p_j$ is the lobe orientation of the $j^{th}$ Lighting SG.
• $\lambda_j$ is the lobe sharpness of the $j^{th}$ Lighting SG.
• $\mu_j$ is the lobe amplitude of the $j^{th}$ Lighting SG.
• $p_D$ is the lobe orientation of the Specular SG.
• $\lambda_D$ is the lobe sharpness of the Specular SG.
• $\mu_D$ is the lobe amplitude of the Specular SG.

Visibility $V(i)$ needs to be calculated.